 |
| 4-Square Diagram |
Greg Ordy
If you have been reading through my web pages such as The RDF Metric, and The Challenge, you know that I have been interested in using the RDF metric to measure the quality of a receiving antenna for the lower frequency bands. RDF is the difference between the maximum gain and the average gain. In most all cases, relatively large RDF values are the result of combining multiple antenna elements into a single antenna system. The individual antenna elements cooperate together to create a focused pattern of response. It is that focusing that causes a difference between maximum and average gain. This sort of antenna system is often called a phased array, because specific current phase relationships exist between the elements. Characteristics of a phased array can be determined from antenna modeling.
When all of the dust settles after the modeling of a phased array antenna, you are left with the specification of one or more sources. Each of these sources (usually the same as an element feed point) has a particular current magnitude and phase, and occurs on an antenna element. If you have a single source, then you usually have a parasitic array. All elements, except the one with the source, receive power from the source element through mutual coupling. In the case of parasitic arrays, the remaining design step is to add some sort of matching network that converts the antenna feed point impedance (at the source) to the impedance of the transmission line.
In the case of multiple sources, an additional design step is needed. A phasing network must be added which combines all of the sources so that the desired current magnitude and phase specifications are present at all sources. The sources are combined to a single antenna feed point, then which connects to the radio with a transmission line. The term feed point is used to describe the entire antenna system single feed point, as well as the feed point of each element.
The design and construction of phasing networks is nontrivial. Over the years, several different design approaches have emerged. The ON4UN book has a good summary of several popular approaches and examples of all of them.
Despite lots of effort and hard work, the result is often errors in the phasing network such that the desired current magnitudes and phases are not realized. Since the current is incorrect, the expected antenna performance will not be realized. The purpose of this web page is to investigate the effect of phasing errors on a typical antenna system, in particular, the effect on RDF.
The effect of phasing errors on other antenna performance metrics is, for the most part, well understood. Some of the metrics are relatively insensitive to phasing errors, and others are extremely sensitive to errors. While I doubt if this one example answers all questions for all arrays, I do believe that the results suggest where RDF falls.
As a quick summary, antenna forward gain is usually considered to be relatively insensitive to (reasonable) phasing network errors. This is often as expressed with the phrase: the antenna wants to work. Even with bent or missing elements, or an incorrect phasing network, the antenna seems to do the job. When it comes to forward gain this is true. On the other hand, a metric which is very sensitive to phasing network errors is the F/B ratio, or more precisely, the depth of signal nulls off of the side and/or rear of the antenna. Small phasing errors can reduce the depth of a null by 20 or more decibels. Even if you have a perfect feed system, null depth will usually be frequency dependent, such that the deep null only occurs over a very narrow frequency range. Nulls are very illusive and hard to control, but they are a wonderful place to direct undesired signals, since the signal will be highly attenuated.
The question on the table becomes, is RDF relatively insensitive to phasing network errors, like forward gain, or, is it very sensitive to errors, as in the case of nulls.
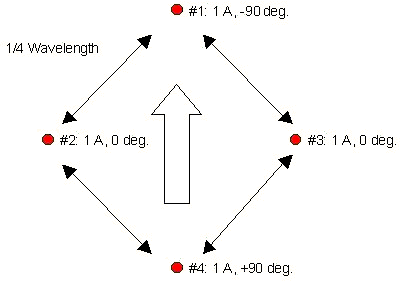
I chose the 4-Square as my example antenna. It has four vertical elements, and has been described in many books and articles. I further used the example provided with the EZNEC software (file 4square.ez), which is a 40 meter 4-Square, designed for 7.150 MHz. Here is a diagram of the classic 4-Square, locating the 4 vertical antenna elements with their desired current magnitudes and phases. This is a view of the antenna if you were looking down at it from above.
 |
| 4-Square Diagram |
The four vertical elements are represented by red circles. The elements are located at the corners of a square which is 1/4 wavelength per side at the desired frequency. The arrow shows the direction of maximum signal, which is through the array on a diagonal line. All four elements have a current magnitude of 1 Amp, but they differ in phase. The element pointing in the forward direction (#1) has a phase of -90 degrees. The two center elements (#2, #3) have a phase of 0 degrees, and the rear element (#4) has a phase of +90 degrees.
Please note that the current magnitudes should really be expressed as a ratio between the elements. The actual current in each element will be related to the transmit power (or receive signal strength), which obviously can be any value. But, it's common practice to use a nominal value such as 1 Amp as a reference. In this example, the correct way to describe the current magnitude is that the four elements have equal current magnitudes, which could be written as: 1 : 1 : 1 : 1. That is, each element has 1 relative unit of current, and all of the current ratios are 1 to 1. I will use that notation in the following tables. The important part of these numbers are their ratios, not their absolute values. A real 4-Square might be 2 : 2 : 2 : 2, or 3.14 : 3.14 : 3.14 : 3.14, or any other current magnitude value. When the antenna is being used for reception, the current in each element will be very, very small.
Phase is also a relative term. For a 4-Square, I like to think of the three phases present as being at -90, 0, and +90 degrees. This is the same as, and often expressed as, 0, 90, and 180 degrees. The phase relationships between the elements are the same. I also use the ratio syntax for describing the phase relationship. In this case, the desired current phases are -90 : 0 : 0 : +90. What matters is the relative phase lead and lag between elements.
In order to simulate the effect of phasing network errors, all I had to do was alter any of the magnitude or phase values in the EZNEC model.
In this section I varied the current magnitude of the center elements. The phase relationship was held constant at -90 : 0 : 0 : +90 degrees (the desired values).
The current in the center elements were set at 60 %, 70 %, 80 %, 90 %, 100 %, 110 %, 120 %, 130 %, and 140 % of the normal (1 Amp) values.
|
Current Magnitude Error Results (4-Square middle elements varied) |
|||||||
| Current Magnitude (%) | RDF (dB) | Gain (dBi) | Take-Off Angle (degrees) | Beamwidth (degrees) | F/B Ratio (dB) | Element Drive Impedance (Ohms) | Element Power (watts) |
|
60 % |
10.66 | 5.32 | 24 | 100.4 | 14.27 | 10.6 - j5.6 40.9 - j21.9 40.9 - j21.9 46.7 +j38.6 |
184 255 255 807 |
|
70 % |
10.68 | 5.39 | 24 | 100.2 | 18.51 | 7.6 - j9.3 40.9 - j21.9 40.9 - j21.9 49.7 +j42.3 |
117 309 309 765 |
|
80 % |
10.64 | 5.4 | 24 | 100.2 | 25.38 | 4.6 - j12.9 40.9 - j21.9 40.9 - j21.9 52.7 +j45.5 |
63 358 358 721 |
|
90 % |
10.57 | 5.38 | 24 | 100.2 | 35.07 | 1.7 - j16.7 40.9 - j21.9 40.9 - j21.9 59.7 +j49.6 |
20 402 402 676 |
|
100 % (design) |
10.49 | 5.34 | 24 | 100.2 | 24.13 | -1.39 - j20.3 40.9 - j21.9 40.9 - j21.9 58.7 +j53.3 |
-15 441 441 633 |
|
110 % |
10.40 | 5.28 | 24 | 100.0 | 19.29 | -4.4 - j24.0 40.9 - j21.9 40.9 - j21.9 61.7 + j57.0 |
-42 475 475 592 |
|
120 % |
10.31 | 5.22 | 24 | 100.0 | 16.42 | -7.3 -j27.7 40.9 - j21.9 40.9 - j21.9 64.7 + j60.7 |
-63 504 504 554 |
|
130 % |
10.21 | 5.14 | 24 | 100.0 | 14.44 | -10.4 - j31.4 40.9 - j21.9 40.9 - j21.9 67.8 + j64.4 |
-80 530 530 519 |
|
140 % |
10.11 | 5.07 | 24 | 100.0 | 12.95 | -13.4 - j35.0 40.9 - j21.9 40.9 - j21.9 70.8 + j68.0 |
-92 553 553 487 |
The drive impedance and power values are shown in order, from element #1 to element #4.
The RDF, Gain, take-off angle, and beamwdith held nearly constant across all current magnitude variations. The F/B ratio, element drive impedance, and element power changed quite a bit. When I first looked at these numbers I was excited that the element power values (in particular, their ratio), could be used as a check of the current magnitude ratios. I believed power could be used for that purpose, but I soon realized that measuring power is not easy, especially in the face of a nonconstant impedance. The most common power meters measure power relative to some specified impedance, usually 50 Ohms. I'm not sure how one would measure power (a scalar quantity) right at the base of each antenna, in the face of changing and reactive feed point impedances. If you have a solution, please let me know.
In the case of magnitudes equal to and above 100 %, the power of the first element is negative. This is entirely allowed, and indicates that the element receives so much power from the other elements through mutual coupling that it actually returns power through the feed system. Note that in all cases the total power still adds to 1500 watts. We are not creating additional power.
In this example, it's interesting to note that when the current magnitude and phase is correct, the first element accepts approximately zero power from the transmitter. This does not mean that the element is unnecessary. An element is unnecessary if its current is zero. Element #1 has nonzero current. The power that is translated into that current comes from the other elements, not the transmitter. While negative power can occur in array elements, especially closely-spaced arrays, it is not often the case that the power will be zero when the phasing is correct.
The center elements (#2 and #3) had a constant drive impedance of 40.9 - j21.9 Ohms. But, the power in the center elements varied. This is because the impedance in the other two elements changed, and that altered the distribution of power.
In this set of simulations, the current magnitudes were set to the design (1 : 1 : 1 : 1) values, but the phase of the center two elements was varied. The designed phase was 0 degrees. The phase variations listed are the deviation from 0 degrees in the center two elements.
|
Current Phase Error Results (4-Square middle elements varied) |
|||||||
| Phase Variation (degrees) | RDF (dB) | Gain (dBi) | Take-Off Angle (degrees) | Beamwidth (degrees) | F/B Ratio (dB) | Element Drive Impedance (Ohms) | Element Power (watts) |
| -20 | 10.38 | 5.23 | 24 | 100.4 | 15.35 | 13.0 - j28.4 40.9 - j21.9 40.9 - j21.9 44.3 +j61.4 |
140 441 441 478 |
| -15 | 10.43 | 5.28 | 24 | 100.4 | 17.71 | 11.5 - j32.9 40.9 - j21.9 40.9 - j21.9 48.2 + j59.9 |
99 441 441 519 |
| -10 | 10.47 | 5.32 | 24 | 100.2 | 20.6 | 5.6 - j25.0 40.9 - j21.9 40.9 - j21.9 51.9 + j58.0 |
59 441 441 559 |
| -5 | 10.49 | 5.34 | 24 | 100.2 | 23.59 | 1.9 - j22.8 40.9 - j21.9 40.9 - j21.9 55.4 + j55.8 |
21 441 441 597 |
| 0 (design) | 10.49 | 5.34 | 24 | 100.2 | 24.13 | -1.39 - j20.3 40.9 - j21.9 40.9 - j21.9 58.7 +j53.3 |
-15 441 441 633 |
| 5 | 10.48 | 5.33 | 24 | 100.0 | 21.44 | -4.48 - j17.5 40.9 - j21.9 40.9 - j21.9 61.8 + j50.6 |
-48 441 441 666 |
| 10 | 10.45 | 5.30 | 24 | 100.0 | 18.43 | -7.3 - j14.5 40.9 - j21.9 40.9 - j21.9 64.7 + j47.6 |
-79 441 441 697 |
| 15 | 10.4 | 5.25 | 24 | 100.0 | 15.94 | -9.9 - j 11.3 40.9 - j21.9 40.9 - j21.9 67.2 + j44.3 |
-107 441 441 725 |
| 20 | 10.33 | 5.18 | 24 | 99.8 | 13.89 | -12.2 - j7.8 40.9 - j21.9 40.9 - j21.9 61.9 + j40.9 |
-131 441 441 749 |
The RDF and Gain varied by a very small amount, less than 0.25 dB. The F/B ratio varied by nearly 11 dB.
In this case, the drive impedance of the center two elements remained the same, and the power in those elements also stayed the same. This is different than in the case of the magnitude errors, where the impedance was constant, but the power in the center two elements changed. In this case, the power stayed constant, although the power did shift in the other two elements. It's also true that in all phase variation cases, the average gain held constant.
I modeled two cases with what I would call extreme errors. These elements have both magnitude and phase errors. In practice, most errors are extreme, in that magnitude and phase tend to change together, and it's very difficult to change one without changing the other.
The first case had current magnitude ratios of 1.0 : 0.7 : 1.4 : 0.9. The two middle elements had a 1 : 2 ratio, as opposed to the expected 1 : 1 ratio, and neither was at 1.0. The fourth element relative current was 0.9, as opposed to the expected 1.0. The phase relationships were also perturbed. The relative phase relationships were -70 : -10 : +20 : +90 degrees, across the four elements.
Even with these large errors, the gain was 5.26 dBi, and the RDF was 10.5 dB, values nearly identical to the case of the ideal feed system. The F/B ratio was only 12.95 dB. The beamwidth actually narrowed compared to the standard case.
The second case also had an imbalance between the center two elements. While RDF and Gain fell off more than in the previous simulations, the reduction was approximately 1 dB.
|
Extreme Error Results |
|||||||
| Current and Phase Ratios | RDF (dB) | Gain (dBi) | Take-Off Angle (degrees) | Beamwidth (degrees) | F/B Ratio (dB) | Element Drive Impedance (Ohms) | Element Power (watts) |
| 1.0:0.7:1.4:0.9 -70, -10, +20, 90 |
10.5 | 5.26 | 24 | 94.1 | 12.95 | -9.7 - j1.7 19.6 - j32.4 37.0 - j7.0 61.9 +j50.0 |
-119 118 888 614 |
| 0.5 :0.6 :1.5 :1.5 -120, -30, -10, 90 |
9.46 | 4.36 | 24 | 122.1 | 24.65 | -27.0 - j55.3 80.4 - j72.3 21.5 - j24.2 46.7 + j28.0 |
-51 219 366 965 |
In some cases, the array no longer points in the expected direction. In the second case, the imbalance between the center two elements caused the direction of maximum gain to shift by over 45 degrees.
Another issue that is important to phased arrays is their bandwidth. For simple antennas, when we talk about bandwidth we usually mean the SWR bandwidth. For phased arrays, an added dimension is the bandwidth over which the phasing network delivers the desired current ratios, or something acceptably close. It is usually the case that changing the frequency will change the current ratios, and therefore the pattern of the antenna. This is a particular problem on 80 meters, where the CW and Phone DX windows are relatively far apart in frequency. Many people spend a lot of time adjusting their antenna system so that the largest nulls will be produced at a desired frequency. The bottom line is that nulls are usually very sensitive to frequency, as well as phase errors.
In order to take a look at the effect of frequency changes on RDF, I switched to a second EZNEC sample model. This one, 4sqtl.ez, is also a 40 meter 4-Square, but it includes a phasing network made up of transmission lines. A set of transmission lines can often times be used as the phasing network, and the transmission line is also a device which can be modeled in EZNEC. It was necessary to switch to a model that included the phasing network so that I could observe the impact of frequency changes on the entire antenna system. In most cases, antenna models of phased arrays (unless they are parasitic) do not include the phasing network. The current ratios are simply supplied as inputs, and they do not change, even when frequency changes. In practice, the current ratios would usually never stay constant as frequency changes. This can lead to overly optimistic estimates of an antenna's performance, as a function of frequency.
I ran a set of simulations of 4sqtl.ez at 7 different frequencies spaced across the United States 40 meter band. The apparent design frequency of the antenna was 7.150 MHz. Here are the results.
| 40 Meter 4-Square Performance Across the Band | |||
| Frequency (MHz) | RDF (dB) | Gain (dBi) | F/B Ratio (dB) |
| 7.000 | 9.74 | 4.75 | 10.83 |
| 7.050 | 9.99 | 4.96 | 12.83 |
| 7.100 | 10.22 | 5.14 | 15.59 |
| 7.150 | 10.41 | 5.28 | 19.46 |
| 7.200 | 10.53 | 5.37 | 23.27 |
| 7.250 | 10.59 | 5.41 | 21.06 |
| 7.300 | 10.59 | 5.41 | 17.04 |
All three metrics fell off as the frequency dropped, but only F/B fell off as the frequency increased. RDF and gain actually drifted slightly higher than at the design frequency of 7.150 MHz. The variation in RDF and gain was less than 0.5 dB. If you wanted to simulate the same percentage change in frequency on 40 meters that occurs on 80 meters (between the CW and Phone DX windows), you would need to consider 6.58 MHz at the low end. At that frequency, the gain was reported as 3.38 dBi, the RDF was 8.23 dB, and the f/B fell sharply to 4.38 dB.
Not all phasing networks are frequency sensitive. Some designs attempt to provide good performance across a frequency span.
[NOTE: The supplied 4sqtl.ez file cannot be used without modification for these measurements. The transmission lines used in the phasing network were specified in degrees, not distance. This means that the electrical length of the transmission lines will stay constant, even as the frequency changes. Real lines have fixed lengths, and their electrical length will change with frequency. Before I recorded this data, I converted the lines to their equivalent physical lengths at the frequency of 7.150 MHz. As the frequency changes, the electrical length of the lines will also change, which is how it is in the real world.]
RDF, like gain, is relatively insensitive to magnitude and phase errors in the feed system. The primary value of getting the feed system correct is sharp and deep nulls, and controllable minimum SWR. The SWR can be reduced by the use of additional matching networks. Still, even in the face of large errors, errors that destroy deep nulls, RDF and gain tend to drop very little. They may drop 1 or 2 dB, whereas nulls may change magnitude by over 30 dB. This should not be too surprising, since RDF is related to forward gain, which we already knew was somewhat insensitive to phasing network errors, and average gain, which would also seem to be a rather general property of the antenna. RDF appears to be relatively insensitive to frequency changes as well.
While all of the results presented come from one particular antenna design, I suspect that the trends hold true for most other phased array antennas.
Although the RDF may not swing as much as the nulls, it's range is much more limited. On my The RDF Metric page, the results indicated that the vast majority of practical receiving antennas had a total RDF span of 5 dB. As a result, a single RDF dB may be more valuable than a gain dB, or null dB. So, it may be very worthwhile to take the time to maximize the RDF, even it is only a dB. This implies that you really should tune up your phasing network, and understand your whole antenna system.
Back to my Experimentation Page